We'll start with the basics by introducting the concept of radians. What exactly are radians?
Radians are an alternative to degrees. Let's make sure that everyone is on the same page, with a quick and fun refresher course in degrees:
Most people are familiar with degrees. They're an absolute necessity when studying things like geography (where on Earth am I?) or astronomy (When will I be able to see a given star from where I am on Earth?). So why do we even need an alternative to degrees?
I'll highlight the problem with a smaller-scale example. Imagine a public park with circular running tracks of varying sizes, and two people, one who is trying to build his speed and stamina for a 100 meter race, and the other person who is timing the runner. They find a track, and the timer stands in the center of the circular track. The runner notes that the circular track is some weird amount, say, 142 meters in circumference, so he needs to know the location of the 100 meter mark.
The timer whips out his calculator, divides 100 by 142, getting 0.704225352. He multiplies this by 360 degrees, since the track is circular, and cheerfully exclaims that all the runner has to do is run 254 degrees (253.521127 degrees, to be more precise) to cover 100 meters on that track. At this point, the runner gives the timer a funny look.
See the problem now? 254 degrees is great when describing how far the timer, standing in the center of the circular track, has to turn to watch the runner. This doesn't help the runner much, as the runner isn't standing in the center. That's the whole thing with degrees; they're great for observers, such as the timer, but not so much for people or things moving around a circumference, such as our runner. This is why there's a need for an alternative to degrees.
Note that the absolute distance of 100 meters isn't of much help, either. On the different sized tracks in the park, that distance will be a different number of laps on each track. So, absolute distance and degrees aren't handy, thus we introduce radians. So what exactly are they?
Since the radius of a circle has a constant relationship with the circumference, that of Pi times twice the radius, how about counting off how far we've traveled around the circumference of a circle in terms of that circle's own “radius units”? It's a good idea, but “radius units” sounds weird (I think it's the repetition of the letter U), so we use the term radians instead!
It boils down to this: 1 radian is simply the length of a circle's radius traveled around that same circle's circumference.
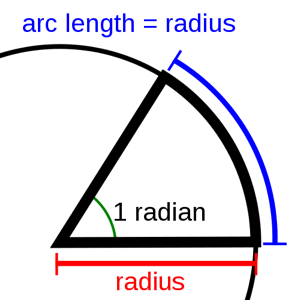
That also gives us the formula to calculate radians: Radians = distance traveled / radius.
Math books like to scare you by writing this same formula as θ = s / r. θ is pronounced “theta”, and simply refers to the answer in radians. s means “arc length”, or, the distance traveled around the circumference. r, the only straightforward shorthand in this formula, means the length of the radius.
Going back briefly to the oberver's point of view, 1 radian translates into about 57.3 degrees (actually 57.29577951... and on and on). For the oberver, this certainly isn't a nice neat number, like 90 degrees, 180 degrees, or 360 degrees. As we've already learned though, the observer's viewpoint is not the point of radians.
However, in the next tab, we'll introduce the unit circle concept itself, and see how radians make things nice and easy for the person or thing that is moving around it.
Radians are an alternative to degrees. Let's make sure that everyone is on the same page, with a quick and fun refresher course in degrees:
Most people are familiar with degrees. They're an absolute necessity when studying things like geography (where on Earth am I?) or astronomy (When will I be able to see a given star from where I am on Earth?). So why do we even need an alternative to degrees?
I'll highlight the problem with a smaller-scale example. Imagine a public park with circular running tracks of varying sizes, and two people, one who is trying to build his speed and stamina for a 100 meter race, and the other person who is timing the runner. They find a track, and the timer stands in the center of the circular track. The runner notes that the circular track is some weird amount, say, 142 meters in circumference, so he needs to know the location of the 100 meter mark.
The timer whips out his calculator, divides 100 by 142, getting 0.704225352. He multiplies this by 360 degrees, since the track is circular, and cheerfully exclaims that all the runner has to do is run 254 degrees (253.521127 degrees, to be more precise) to cover 100 meters on that track. At this point, the runner gives the timer a funny look.
See the problem now? 254 degrees is great when describing how far the timer, standing in the center of the circular track, has to turn to watch the runner. This doesn't help the runner much, as the runner isn't standing in the center. That's the whole thing with degrees; they're great for observers, such as the timer, but not so much for people or things moving around a circumference, such as our runner. This is why there's a need for an alternative to degrees.
Note that the absolute distance of 100 meters isn't of much help, either. On the different sized tracks in the park, that distance will be a different number of laps on each track. So, absolute distance and degrees aren't handy, thus we introduce radians. So what exactly are they?
Since the radius of a circle has a constant relationship with the circumference, that of Pi times twice the radius, how about counting off how far we've traveled around the circumference of a circle in terms of that circle's own “radius units”? It's a good idea, but “radius units” sounds weird (I think it's the repetition of the letter U), so we use the term radians instead!
It boils down to this: 1 radian is simply the length of a circle's radius traveled around that same circle's circumference.

That also gives us the formula to calculate radians: Radians = distance traveled / radius.
Math books like to scare you by writing this same formula as θ = s / r. θ is pronounced “theta”, and simply refers to the answer in radians. s means “arc length”, or, the distance traveled around the circumference. r, the only straightforward shorthand in this formula, means the length of the radius.
Going back briefly to the oberver's point of view, 1 radian translates into about 57.3 degrees (actually 57.29577951... and on and on). For the oberver, this certainly isn't a nice neat number, like 90 degrees, 180 degrees, or 360 degrees. As we've already learned though, the observer's viewpoint is not the point of radians.
However, in the next tab, we'll introduce the unit circle concept itself, and see how radians make things nice and easy for the person or thing that is moving around it.
Since we now have the scalable concept of radians to work with, we can now develop an entire scalable circle with which to work. We'll start by drawing on graph paper a circle centered at the (0,0) mark that has a 1 unit radius (remember cartesian coordinates?). It looks at it does below, with the coordinates marked where it crosses an axis:

That fact that it's a circle with a one-unit radius gives us the shorthand term for it: unit circle. Let's take a closer look at it what a unit circle can do.
Here's your first question: Since radians measure how far around a circle you've traveled, what's the distance around a full unit circle in radians? Let's work this out.
Our circle has a radius of 1 unit, so the circumference (our total distance traveled, in this case) is 2 times the radius times Pi, so we have 2 times 1 unit, giving 2 units, times Pi, resulting in 2 * Pi, or 2π for short (That π symbol is the Pi symbol, not a small letter n). That's just the total distance traveled, though.
To convert that to radians, we need to divide by the radius, of course. Our radius is 1 unit, so we work out 2π/1, which is simply 2π. In other words, the distance around a full circle is 2π radians in length!
Now you see why 1 radian is such a weird angle in degrees (1 radian = 57.29577951... degrees). When doubled and multiplied by Pi, it has to give a nice even 360 degrees. Again, we're going to stick to radians in this discussion, so just think of 2π radians as a full circle.
From here, it's not hard to see that π radians gives us half of a circle, and π/2 radians gives us a quarter circle. Three-quarters of a circle, then, would give us a distance of 3π/2 radians.
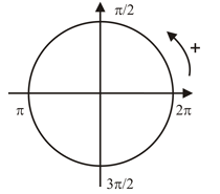
So, what distances are we traveling in radians when we traveling 45 degrees? 45 degrees is the centered observer's way of saying an eighth of a circle. The mover thinks of a circle as being 2π radians, so 2π times 1/8 would be 2π/8, or the same as π/4 radians.
Every 1/8 of a trip around the circle, then, would be in units of π/4 radians:
Since angles of 30 degrees, or 1/12 of the distance around the circle, are also common, they're not hard to work out in radians. 1/12 of 2π radians comes down to π/6 radians. From there, we get:
So, if you can remember that 2π radians takes you all the way around the circle, and that π radians, as well as 6π/6 and 4π/4 radians, takes you halfway around the circle, working out the rest of the numbers isn't difficult at all.
In the next tab, we'll discuss another amazing way the unit circle becomes useful when we focus on figuring out coordinates.

That fact that it's a circle with a one-unit radius gives us the shorthand term for it: unit circle. Let's take a closer look at it what a unit circle can do.
Here's your first question: Since radians measure how far around a circle you've traveled, what's the distance around a full unit circle in radians? Let's work this out.
Our circle has a radius of 1 unit, so the circumference (our total distance traveled, in this case) is 2 times the radius times Pi, so we have 2 times 1 unit, giving 2 units, times Pi, resulting in 2 * Pi, or 2π for short (That π symbol is the Pi symbol, not a small letter n). That's just the total distance traveled, though.
To convert that to radians, we need to divide by the radius, of course. Our radius is 1 unit, so we work out 2π/1, which is simply 2π. In other words, the distance around a full circle is 2π radians in length!
Now you see why 1 radian is such a weird angle in degrees (1 radian = 57.29577951... degrees). When doubled and multiplied by Pi, it has to give a nice even 360 degrees. Again, we're going to stick to radians in this discussion, so just think of 2π radians as a full circle.
From here, it's not hard to see that π radians gives us half of a circle, and π/2 radians gives us a quarter circle. Three-quarters of a circle, then, would give us a distance of 3π/2 radians.

So, what distances are we traveling in radians when we traveling 45 degrees? 45 degrees is the centered observer's way of saying an eighth of a circle. The mover thinks of a circle as being 2π radians, so 2π times 1/8 would be 2π/8, or the same as π/4 radians.
Every 1/8 of a trip around the circle, then, would be in units of π/4 radians:
- 1/8 = π/4 radians
- 2/8 = 2π/4 = π/2 radians
- 3/8 = 3π/4 radians
- 4/8 = 4π/4 = &pi radians
- 5/8 = 5π/4 radians
- 6/8 = 6π/4 = 3π/2 radians
- 7/8 = 7π/4 radians
- 8/8 = 8π/4 = 2π radians
Since angles of 30 degrees, or 1/12 of the distance around the circle, are also common, they're not hard to work out in radians. 1/12 of 2π radians comes down to π/6 radians. From there, we get:
- 1/12 = π/6 radians
- 2/12 = 2π/6 = π/3 radians
- 3/12 = 3π/6 = π/2 radians
- 4/12 = 4π/6 = 2π/3 radians
- 5/12 = 5π/6 radians
- 6/12 = 6π/6 = π radians
- 7/12 = 7π/6 radians
- 8/12 = 8π/6 = 4π/3 radians
- 9/12 = 9π/6 = 3π/2 radians
- 10/12 = 10π/6 = 5π/3 radians
- 11/12 = 11π/6 radians
- 12/12 = 12π/6 = 2π radians

So, if you can remember that 2π radians takes you all the way around the circle, and that π radians, as well as 6π/6 and 4π/4 radians, takes you halfway around the circle, working out the rest of the numbers isn't difficult at all.
In the next tab, we'll discuss another amazing way the unit circle becomes useful when we focus on figuring out coordinates.
I have some quick refresher questions before we move on. When you've traveled π/2 radians, at what (x,y) coordinates are you? You're at (0,1).
Here's a tougher one: When you've traveled π/4 radians, at what (x,y) coordinates are you? That one's a little trickier. For this one, we're going to have to go back the viewpoint of the observer in the center, and thus back to degrees.
The radius of the unit circle is, of course, always 1 unit. If we construct a right triangle with the radius line as the hypotenuse, we could construct a right triangle for any angle in the circle:
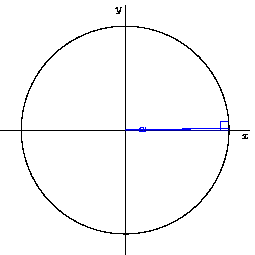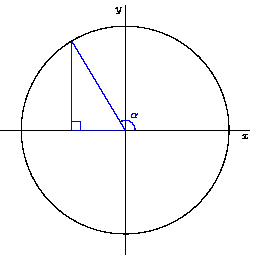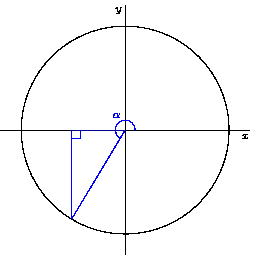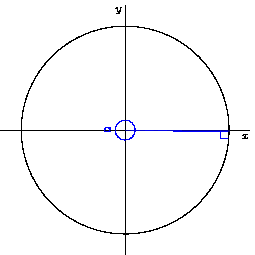
Since π/4 radians from the central observer's point of view is 45 degrees, we'll create a 45 degree right triangle to help work out those coordinates:
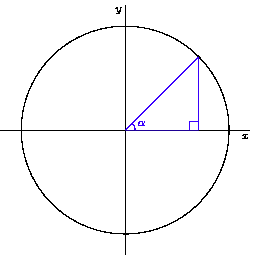
Since we're looking for the (x,y) coordinate, the length of the side adjacent to our angle (the one running along the x axis) would give us the x coordinate. The height of the side opposite the angle (the one running straight up to meet the radius/hypotenuse) would give us the y coordinate.
If you remember all those lessons about right triangles, it's at this point where you begin to realize how many tools we can use here.
Since the hypotenuse is 1, and both the sine and cosine divide by the hypotenuse, not only does this make the math nice and easy, but the answers will also be the exact coordinates we need!
The x coordinate is the length of the side adjacent to the angle, so we need to use the cosine formula. By cheating and using a calculator (make sure to set it in degrees, not radians!) we find that cos(45 degrees) = 0.707106781.... To get the y coordinate, we find the length of the side opposite the angle by using sin(45 degrees), which is also 0.707106781....
So, we have our coordinates for a 45 degree, or π/4 radian, angle: (0.707106781...,0.707106781...). Hmmm, that's another one of those numbers that goes on forever. Isn't there a better way to state that number?
Let's run through the Pythagorean Theorem approach, especially know that we know that sides a and b are equal, and see what we can come up with:
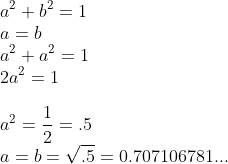
“OK,” you say, “so what? We just came up with the same numbers.” Let's back up a bit to to where a squared (and b squared, in the specific case of a 45 degree right triangle) was equal to 1/2. Instead of using .5, let's see where working with that 1/2 as a fraction can take us:
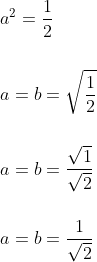
Hmmm...writing one over the square root of 2 is certainly much easier than that long string of numbers. Indeed, when you're tested on unit circles on many standardized tests, they'll usually ask you to write the π/4 radian or 45-degree coordinate in exactly that way.
Before moving on, though, I'd like to make that fraction a bit neater by making the bottom a whole number. We do that by multiplying both the top and bottom by the square root of two, and expressing the coordinates as fractions:
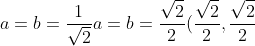)
Not only is this a cleaner way to write the coordinates, it will make this and the other coordinates we work out much easier to remember, as you'll see in later sections.
The fractions may look funny, but all they're really saying is, “If you take the square root of 2, and divide it in half, that's a shortcut to working out this coordinate.” Or, put the opposite way, “Hey, if you take this coordinate, double it, and then square it, you get a nice, simple number, in this case - 2!”
We'll work out the coordinates and their corresponding fractions for the 30- and 60-degree angles in the next section, as well as their multiples.
Here's a tougher one: When you've traveled π/4 radians, at what (x,y) coordinates are you? That one's a little trickier. For this one, we're going to have to go back the viewpoint of the observer in the center, and thus back to degrees.
The radius of the unit circle is, of course, always 1 unit. If we construct a right triangle with the radius line as the hypotenuse, we could construct a right triangle for any angle in the circle:

Since π/4 radians from the central observer's point of view is 45 degrees, we'll create a 45 degree right triangle to help work out those coordinates:

Since we're looking for the (x,y) coordinate, the length of the side adjacent to our angle (the one running along the x axis) would give us the x coordinate. The height of the side opposite the angle (the one running straight up to meet the radius/hypotenuse) would give us the y coordinate.
If you remember all those lessons about right triangles, it's at this point where you begin to realize how many tools we can use here.
- Pythagorean Theorem: a2 + b2 = c2
- Sine of any angle = opposite/hypotenuse
- Cosine of any angle = adjacent/hypotenuse
Since the hypotenuse is 1, and both the sine and cosine divide by the hypotenuse, not only does this make the math nice and easy, but the answers will also be the exact coordinates we need!
The x coordinate is the length of the side adjacent to the angle, so we need to use the cosine formula. By cheating and using a calculator (make sure to set it in degrees, not radians!) we find that cos(45 degrees) = 0.707106781.... To get the y coordinate, we find the length of the side opposite the angle by using sin(45 degrees), which is also 0.707106781....
So, we have our coordinates for a 45 degree, or π/4 radian, angle: (0.707106781...,0.707106781...). Hmmm, that's another one of those numbers that goes on forever. Isn't there a better way to state that number?
Let's run through the Pythagorean Theorem approach, especially know that we know that sides a and b are equal, and see what we can come up with:
“OK,” you say, “so what? We just came up with the same numbers.” Let's back up a bit to to where a squared (and b squared, in the specific case of a 45 degree right triangle) was equal to 1/2. Instead of using .5, let's see where working with that 1/2 as a fraction can take us:
Hmmm...writing one over the square root of 2 is certainly much easier than that long string of numbers. Indeed, when you're tested on unit circles on many standardized tests, they'll usually ask you to write the π/4 radian or 45-degree coordinate in exactly that way.
Before moving on, though, I'd like to make that fraction a bit neater by making the bottom a whole number. We do that by multiplying both the top and bottom by the square root of two, and expressing the coordinates as fractions:
Not only is this a cleaner way to write the coordinates, it will make this and the other coordinates we work out much easier to remember, as you'll see in later sections.
The fractions may look funny, but all they're really saying is, “If you take the square root of 2, and divide it in half, that's a shortcut to working out this coordinate.” Or, put the opposite way, “Hey, if you take this coordinate, double it, and then square it, you get a nice, simple number, in this case - 2!”
We'll work out the coordinates and their corresponding fractions for the 30- and 60-degree angles in the next section, as well as their multiples.
So, now we not only know the coordinates for a 45 degree, or π/4 radian, point on a circle, we know that the cosine will give us the x coordinate and that the sine will give us the y coordinate on the unit circle. We also know that expressing these coordinates in fractions is much simpler than writing out the endless irrational decimals.
Let's work out the coordinates for the point at 30 degrees (π/6 radians):
 = 0.866025404...\\ sin(30^{\circ}) = 0.5\\ (0.866025404..., 0.5)\\ \\ (0.866025404..., \frac{1}{2})\\)
Hey! That .5 is nice. That's easy to express as a fraction. But what about that other number? Well, everything else has been expressed over 2, so let's see what happens when we express that number over 2:
\\)
Ummm...yuck. Well, square roots seem to be popular in these fractions. Is 1.73205081... the square root of anything? Yep! It turns out that it's the square root of 3! So, the coordinates could be expressed this way:
\\)
Next, let's work out the coordinates for 60 degrees (π/3 radians):
 = 0.5\\ sin(60^{\circ}) = 0.866025404...\\ (0.5, 0.866025404...)\\ \\ (\frac{1}{2}, \frac{\sqrt{3}}{2} )\\)
Whoah! We get the same numbers as the 30 degree angle, only switched! That's not a coincidence. Remember that the internal angles of triangles always add up to 180 degrees. With a right triangle (a triangle with a 90 degree angle in it) that has a 30 degree angle in it, we find that 180 - 90 - 30 = 60 degrees, the remaining angle. Effectively, the 60 degree coordinates are just the 30 degree coordinates viewed from the other side of the triangle.
Let's review all the information, including the coordinates, that we know so far:
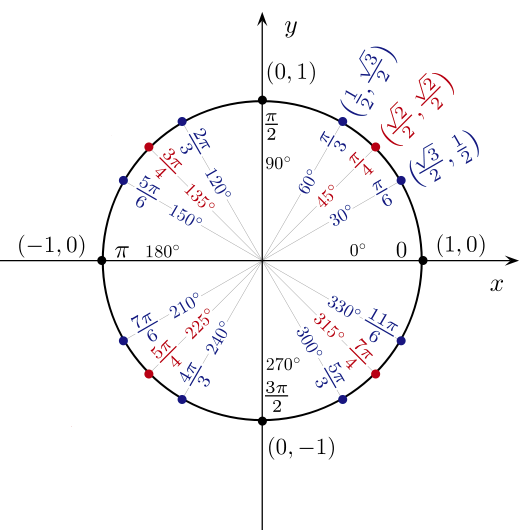
If you think of 1 as also being the square root of 1, you could write 1/2 this way:
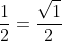
So, at all the points where the circle crosses an axis, the coordinates involve 0, +1, or -1 - Simple! And at the oft-used 30° (π/6 radians), 45° (π/4 radians), and 60° (π/6 radians), all the coordinates involve these interesting fractions:
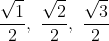
See that? Everything in the fractions is a square root of something over 2! Even better, there's a simple 1, 2, 3 progression! Even with all the complex math involved, it's all boiling down to 0, 1, 2, and 3.
That's easy enough to remember, but how do you remember which fractions are set at which coordinates, especially since it's not hard to make a mistake and switch around the coordinates for both 30° and 60°? Here's a video that will teach you quickly, using that 1, 2, 3 progression:
What about all the remaining major angles, such as 120°, 135°, and so on?
Well, you could go through and work out the coordinates laboriously as we did above, working out the sines and cosines, and so on. However, there's an easier way. We're measuring the 135° (3π/4 radians) angle from the 0° angle. When measured from the 180° (π radians) angle, it works out to be our old friend, the 45° (π/4 radians) angle.
One difference, though, is that we're now on the negative side of the x axis, so that the x coordinate will be negative. The means the coordinate for the 135° (3π/4 radians) angle will be:
)
Similarly, you can work out the 150° angle as a 30° angle, and so on. They work out to the coordinates we've already determined, but you need to make sure that you adjust the signs (+ or -) for the appropriate section.
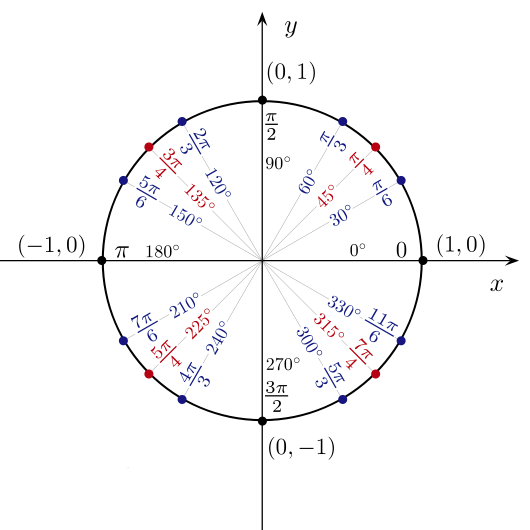
Are you ready for this? Here's the entire unit circle worked out:
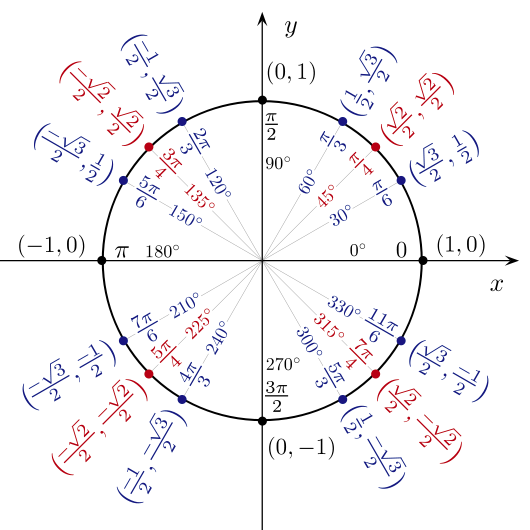
And here's how to draw it that so you remember all that data:
I like the approach used in this video of counting the π/3, π/4, and π/6 sections separately, so as to keep them mentally separate.
In the next tab, I'll review and break down the patterns for easier understanding. You'll also learn how to do some quick math on your fingers to get the coordinates.
Let's work out the coordinates for the point at 30 degrees (π/6 radians):
Hey! That .5 is nice. That's easy to express as a fraction. But what about that other number? Well, everything else has been expressed over 2, so let's see what happens when we express that number over 2:
Ummm...yuck. Well, square roots seem to be popular in these fractions. Is 1.73205081... the square root of anything? Yep! It turns out that it's the square root of 3! So, the coordinates could be expressed this way:
Next, let's work out the coordinates for 60 degrees (π/3 radians):
Whoah! We get the same numbers as the 30 degree angle, only switched! That's not a coincidence. Remember that the internal angles of triangles always add up to 180 degrees. With a right triangle (a triangle with a 90 degree angle in it) that has a 30 degree angle in it, we find that 180 - 90 - 30 = 60 degrees, the remaining angle. Effectively, the 60 degree coordinates are just the 30 degree coordinates viewed from the other side of the triangle.
Let's review all the information, including the coordinates, that we know so far:

If you think of 1 as also being the square root of 1, you could write 1/2 this way:
So, at all the points where the circle crosses an axis, the coordinates involve 0, +1, or -1 - Simple! And at the oft-used 30° (π/6 radians), 45° (π/4 radians), and 60° (π/6 radians), all the coordinates involve these interesting fractions:
See that? Everything in the fractions is a square root of something over 2! Even better, there's a simple 1, 2, 3 progression! Even with all the complex math involved, it's all boiling down to 0, 1, 2, and 3.
That's easy enough to remember, but how do you remember which fractions are set at which coordinates, especially since it's not hard to make a mistake and switch around the coordinates for both 30° and 60°? Here's a video that will teach you quickly, using that 1, 2, 3 progression:
What about all the remaining major angles, such as 120°, 135°, and so on?
Well, you could go through and work out the coordinates laboriously as we did above, working out the sines and cosines, and so on. However, there's an easier way. We're measuring the 135° (3π/4 radians) angle from the 0° angle. When measured from the 180° (π radians) angle, it works out to be our old friend, the 45° (π/4 radians) angle.
One difference, though, is that we're now on the negative side of the x axis, so that the x coordinate will be negative. The means the coordinate for the 135° (3π/4 radians) angle will be:
Similarly, you can work out the 150° angle as a 30° angle, and so on. They work out to the coordinates we've already determined, but you need to make sure that you adjust the signs (+ or -) for the appropriate section.
Are you ready for this? Here's the entire unit circle worked out:

And here's how to draw it that so you remember all that data:
I like the approach used in this video of counting the π/3, π/4, and π/6 sections separately, so as to keep them mentally separate.
In the next tab, I'll review and break down the patterns for easier understanding. You'll also learn how to do some quick math on your fingers to get the coordinates.
It may seem like a lot that you've learned so far, but it boils down to a few basic things:
Betterexplained.com has a wonderful article you should read at this point, called Intuitive Guide to Angles, Degrees and Radians.
It really drives home the power of radians. Take this example from the article:
Think of the power you have here. Sure, the unit circle seems complex at first, but the power and patterns it presents when remembered and understood make many things simple.
Scaling up to real-world circles and back down to the unit of circles, as well as determining their motion, becomes a simple matter of multiplication. You can work out sines, cosines, tangents, and cotangents on your fingers.
Converting from radians to degrees and back, with a little practice, isn't difficult.
Which brings to mind the question of practice. The simplest practice I can offer is to print out several copies of this PDF, and repeatedly fill it out until you're good enough to do so in under 5 minutes, just as it says.
Sporcle offer this ingenious quiz for practicing radians and degrees. With help from the videos from the previous tab, this shouldn't be too tough.
The most complete quiz on the unit circle that I've found, however, is Math Fanatic's Unit Circle and Trigonometry Quiz. The menu lets you select exactly what aspects you want to practice, and the quiz itself lets you practice each section for as long as you need or want. Since it covers most of trigonometry, and not just the unit circle, there will be some quizzes not covered in my unit circle tutorial.
I hope you find this useful, and I also hope it helped you better understand the unit circle.
- Degrees deal with the observer's point of view. Radians deal with the mover's point of view.
- 1 radian = 1 radius length around the circle's circumference.
- Radians work very well with Pi, to the extent that π radians = 180 degrees, and 2π radians = 360 degrees.
- If you think of π radians as being 180 degrees, and you know your multiples of 30 and 45, the remaining degree angles aren't difficult to work out in radians.
- All the coordinate points where the circle cross an axis involve a 0, a -1, or a +1. Knowing coordinates makes it easy to work out which is which.
- All the coordinate points of π/6 (30°), π/4 (45°), and π/3 (60°) radians involve fractions easily remembered with the 1, 2, 3 progression taught in the video in the previous tab.
- The other major coordinate points can be worked out quite easily from those first 3 sets, as long as you adjust the signs properly.
- Cosine will always give the x coordinate on the unit circle, and sine will always give the y coordinate on the unit circle.
Betterexplained.com has a wonderful article you should read at this point, called Intuitive Guide to Angles, Degrees and Radians.
It really drives home the power of radians. Take this example from the article:
Let’s try a real example: you have a bus with wheels of radius 2 meters (it’s a monster truck bus). I’ll say how fast the wheels are turning and you say how fast the bus is moving. Ready?I'm not sure that's the reason they sing about 24″ rims, but I'll go along with it while it lasts.
“The wheels are turning 2000 degrees per second”. You’d think:
Ok, the wheels are going 2000 degrees per second. That means it’s turning 2000/360 or 5 and 5/9ths rotations per second. Circumference = 2 * pi * r, so it’s moving, um, 2 * 3.14 * 5 and 5/9ths… where’s my calculator…“The wheels are turning 6 radians per second”. You’d think:
Radians are distance along a unit circle — we just scale by the real radius to see how far we’ve gone. 6 * 2 = 12 meters per second. Next question.Wow! No crazy formulas, no pi floating around — just multiply to convert rotational speed to linear speed. All because radians speak in terms of the mover.
The reverse is easy too. Suppose you’re cruising 90 feet per second on the highway (60 miles per hour) on your 24″ inch rims (radius 1 foot). How fast are the wheels turning?
Well, 90 feet per second / 1 foot radius = 90 radians per second.
That was easy. I suspect rappers sing about 24″ rims for this very reason.
Think of the power you have here. Sure, the unit circle seems complex at first, but the power and patterns it presents when remembered and understood make many things simple.
Scaling up to real-world circles and back down to the unit of circles, as well as determining their motion, becomes a simple matter of multiplication. You can work out sines, cosines, tangents, and cotangents on your fingers.
Converting from radians to degrees and back, with a little practice, isn't difficult.
Which brings to mind the question of practice. The simplest practice I can offer is to print out several copies of this PDF, and repeatedly fill it out until you're good enough to do so in under 5 minutes, just as it says.
Sporcle offer this ingenious quiz for practicing radians and degrees. With help from the videos from the previous tab, this shouldn't be too tough.
The most complete quiz on the unit circle that I've found, however, is Math Fanatic's Unit Circle and Trigonometry Quiz. The menu lets you select exactly what aspects you want to practice, and the quiz itself lets you practice each section for as long as you need or want. Since it covers most of trigonometry, and not just the unit circle, there will be some quizzes not covered in my unit circle tutorial.
I hope you find this useful, and I also hope it helped you better understand the unit circle.




1 Response to The Unit Circle
I have read news on technical sites that GiveBIG is now dominating the spring fundraising season for most nonprofits in every sector in Seattle and King County. The nonprofit community and fundraising thought leaders are trying to make sense of the GiveLocalAmerica kerfuffle. Great!!Jogo para criança online
play Games friv
free online friv Games
Post a Comment