Introduction

This tutorial is meant as a sequel to my unit circle tutorial. Much of this tutorial assumes you have already been through that one, so if haven't already done so, please go through the previous tutorial now.

The unit circle is meant as a sort of idealized circle, from which all other measurements can be scaled up. Radians, for example, made it easy to determine how far a wheel was traveling, given its rotation in radians. All that was required was a single multiplication.

As a matter of fact, all the measurements on the unit circle work this way. Sine and cosine can be applied to real world measurements with a single multiplication to scale them up or down.

That's why, in the unit circle, all the trigonometric functions do a sort of double duty. They're ratios, as you've been taught, but in the idealized world of the unit circle, they can also be treated as absolutes, since they result in useful coordinates. For example, sine and cosine are both ratios that relate in different ways to the length of the hypotenuse, but also give exact coordinates to graph.

In this tutorial, we'll go beyond sine and cosine, and explore the other trigonometric functions of tangent, cotangent, secant, and cosecant. The goal of this tutorial is to explain them in a way that can be easily understood, comprehended, and remembered.

To explain these, we're going to scale the triangle up beyond the bounds of the unit circle. In the previous tutorial, the hypotenuse always had a length of 1 because it was representing the radius of the unit circle.

The hypotenuse of a right triangle is, by definition, the longest of the three sides, so this meant that, with any given angle, the other two side must always fall on or inside the unit circle itself, because they have to be 1 (in the case of 90 degree or π/2 angles) or less.

What happens, though, if we scale up a right triangle in the unit circle so that the width or height is 1 instead of the hypotenuse? In this tutorial, we'll try that out, and examine the useful measurements that result.

To start off simply, however, we'll focus on the one thing that doesn't change as the right triangle is scaled up - its slope.

Slope

Question: What's the slope of a 30 degree angle? Many would answer something like, “What kind of question is that? It's 30 degrees!“

I'd give that answer half credit. It does recognize that, regardless of the lengths of the sides of the triangle, the slope does remain the same.

However, slope is usually stated as decimal number, so that it's easy to multiply by. Here's a quick refresher course in slope, excerpted from the series The Mechanical Universe:


“Change in elevation” over “change in horizontal distance” is usually stated in a way that's catchier and easier to remember:



For example, take a 45 degree angle in the unit circle. When the hypotenuse was 1 (the radius of the unit circle), what was the rise and what was the run? If you remember the hand trick from the video, it shouldn't be too hard to recall:



So, for a 45-degree angle the slope is 1. In other words, for every 1 unit you move horizontally, you're going to move 1 unit vertically, as well. This makes sense for a 45-degree right triangle, since the two shorter sides are the same length.

What about that 30-degree angle I asked about earlier? Lets work through that problem:



You can see a more exact answer at Wolfram|Alpha. It can also be stated as the square root of 3 over 3.

As you'll see it again and again, you should find a way to remember the square root of 3.

The number is less exact than in our 45-degree answer, but the meaning remains the same. With a 30-degree angle, for every 1 unit you run (move horizontally), you're going to rise (move vertically) 0.57735... units. That's more than half a unit, but less than a slope of 0.60.

We've been talking quite a bit about slope, but not much about the unit circle here. This is a very important tangent however, as you'll learn in the next section.

Tangent

Ever been told by someone that you're going off on a tangent? Ultimately, the complaint is that you're going off on a line that will only take the discussion farther and farther from the main point.

It's almost exactly the same definition in math. One mathematical definition of tangent is a line that touches a circle (a unit circle, for our purposes) at only one point. Starting at that one point, and then traveling along the tangent would only take you farther and farther away from that main point.



As you can see, a tangent is easy to draw. Draw a radius line at any angle, and at the point where it touches the circle, draw a line perpendicular (at a 90° angle) to the radius, and that's the tangent.

To keep things simple in this tutorial, we're only going to consider the horizontal and vertical tangents. In this particular section, we'll only focus on the vertical tangent.

The formula to graph a vertical tangent is easy, it's x=1. When y=0, x=1. When y=5, x=1. When y=4,287, x=1. You get the idea. Not surprisingly, the only point at which it intersects the unit circle is

In the previous tutorial, we always created the length of the hypotenuse (the longest side) to be 1. Imagine that, instead of the hypotenuse having length 1, we had the base have a length of 1.

Here's a picture of the situation:



Here's a question for you: If we tried scaling up a 45° right triangle in this manner, what would the coordinates be where the hypotenuse of this new larger triangle intersects the tangent line?

Let's think about this. Because the tangent is defined as x=1, the x coordinate where the hypotenuse intersects the tangent will also obviously be x=1. So, the coordinates we have so far are (1, something). That's half the work already done!

In the previous section, we worked out that the slope of a 45° angle was 1, at that meant that for every 1 unit you moved horizontally, you moved 1 unit vertically. As it happens, a base width of 1 means we are moving over 1 unit horizontally, so we should obviously move up 1 unit vertically!

So, the coordinates of a 45° angle where it intersects the tangent line would simply by (1,1)!

Did that seem easier than it should have? Let's try it with our 30° angle example, too. What was the slope of that angle? It was 0.57735... and so on. Let's take a look at that angle plotted by Wolfram|Alpha.

That means, for every 1 unit we travel horizontally, we travel 0.57735... units vertically. Yep, the coordinates where the hypotenuse meets the tangent line is (1, 0.57735...).

See the pattern? Whenever a right triangle with a given angle has a base length of 1 in the unit circle, the coordinates where the hypotenuse will intersect the vertical tangent line is (1, slope of that angle)!

As with sine and cosine in the unit circle, the slope is doing double duty. It's both the slope itself, and the y coordinate where the hypotenuse intersects the tangent at x=1. In fact, we could just call this number the tangent.

Remember SOHCAHTOA? That helps remind us, among other things that the formula for the tangent is the opposite side's length over the adjacent side's length. Also, remember that those lengths on the unit circle are worked out by figuring sine (the height) and the cosine (the width)

Let's take a closer look at the formulas for slope and tangent:



Yep, the tangent and the slope are always the same, which is why it works out as it does! This should also help you better understand the brief reference to figuring out tangent on your fingers from the previous tutorial.

So far, we've only dealt with scaling triangles up to meet a vertical tangent. What happens if we scale them up to meet a horizontal tangent?

Horizontal Tangent

With a horizontal tangent, we're simply dealing with what happens when y=1, instead of x=1.

Remember how we determined the tangent (the same as the slope) of a 45° angle was 1, so the coordinates where the hypotenuse met the vertical tangent was (1,1)? For a 45°, this works out nicely, since it intersects the horizontal tangent in the same place.

Let's go back to our 30° example, and get a better idea of what changes. The slope is 0.57735..., so let's view what happens when we try this out:



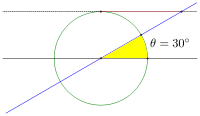
Here's another look at the same situation, via Wolfram|Alpha (albeit slightly distorted). Even without knowing the exact coordinates, we can see that the hypotenuse, in the 30° case, is MUCH longer than where it intersected the vertical tangent.

So, what are the coordinates? We start in a manner similar to before, with the coordinates (something, 1), because the horizontal tangent formula is y=1 (instead of x=1 for the vertical tangent).

In the case of the vertical tangent, we just multiplied 1 (the x coordinate) times the slope to get the y coordinate. Since we're still talking about the same 30° angle, the slope is still the same 0.57735... we used before. We'll just have to come at it from the other way:



You can actually see several important things here. First, we found the coordinates for where our 30° angle intersects the horizontal tangent at (1.73205...,1). Second, while the tangent relationship of y = x × 0.57735... still holds, it would seem easier just to state the relationship the other way around, as in x = y × 1.73205..., especially when that lets you multiply by 1.

Finally, note that you can always find where the hypotenuse intersects the horizontal tangent by dividing 1 by the tangent of the same angle. That's why this number is given the name cotangent.

If you think about it, there are several ways to find the cotangent:



As a brief review, we covered sine and cosine in the previous tutorial, and now we've covered tangent and cotangent. If you think of the horizontal tangent as being a cotangent line, then this is easier to understand.

We keep talking about the slope of the hypotenuse and the coordinates where the hypotenuse intersects the tangent and cotangent lines, but what happens to the length of the hypotenuse as triangles are scaled up to meet the tangent and cotangent lines? That's discussed in the next section.

Hypotenuse Length

We're going to switch from focusing on the slope of the hypotenuse to its length.

This almost means a return to our old friend from the right-triangle, the Pythagorean Theorem: a² + b² = c².

When the hypotenuse is 1 unit long, the squares of the other two sides must add up to 1. For example, in our 30° angle, where the cosine (width) is 0.8660... and the sine (height) is 0.5, we get:



However, the hypotenuse must get longer to meet the tangent lines as we've seen. Let's start as before, scaling up to meet the tangent line (that's the vertical tangent). We've already seen that the coordinates of a 30° angle gives us coordinates of (1, 0.57735...). As in the above example, we note that the coordinates are also the lengths of the two smaller sides. That being the case, let's figure out how long the hypotenuse is when it meets the vertical tangent:



So, we see that the hypotenuse is now 1.1547... units long. Since the original hypotenuse was only 1 unit long, this is a sort of scaling factor for the hypotenuse.

Take another look, though. When we scaled the width of a 30° right triangle from 0.866... to 1, that's a factor of 1.1547... times, as well. The height went from 0.5 units to 0.57735... units, which is also a scaling factor of 1.1547... times!

So, this one factor, when scaling a right triangle up to meet the tangent line tells us how to scale the lengths of all the sides in order to do so! Since we're scaling up from a hypotenuse of 1, this factor also gives us the exact length of the hypotenuse after being scaled up to the tangent line.

In trigonometry, this factor is called the secant. Since we scale the width of the triangle (the cosine, in the unit triangle) up to 1, it shouldn't be surprising that we can find the secant in this manner:



The hypotenuse length was 1 before scaling it up, so you could also work it out by dividing the hypotenuse by the width:

Meeting the Cotangent Line

Let's not forget the length of hypotenuse when scaled up to meet the cotangent line (that's the horizontal tangent line).

Our example 30° right triangle, when scaled up to meet the cotangent line, we found the coordinates (and side lengths) of (1.73205...,1). Let's run the numbers just as before, and find the hypotenuse length:



Oh! The hypotenuse in this case is exactly 2 units long. We took the height (the sine) from 0.5 to 1, which is a factor of exactly 2 units, so we shouldn't be surprised when the hypotenuse (and the width, for that matter) scales up by a factor of 2 units.

Since this scaling factor deals with scaling the height up to the cotangent line, this factor is naturally called the cosecant. The formulas for cosecant are as follows:



At this point, you should understand all 6 trigonometric functions: sine, cosine, tangent, cotangent, secant and cosecant. Once understood, however, they can be easily confused. In our final section, I'll offer some mnemonics to help keep them all straight.

Mnemonics

When you have the explanations and formulas in front of you, it's much easier to keep these things straight. How is it possible to keep all this straight in your head?

Let's break things up several ways. First, by the pairs in which you learned them.

Sine and cosine can be thought of as the simple lengths of the sides in the unit circle, when the hypotenuse is 1. Think of signs that tell you the length of a road.

Tangent and cotangent deal with the unit coordinates when the triangles are scaled up to meet the tangent and the cotangent lines respectively. This is its own mnemonic: tangents deal with tangents.

Secant and cosecant are the scaling factors to the tangent and cotangent lines respectively. Think secant means “secaling” factor.

Once you get the functions themselves straight, it can seem tricky to remember which of each pair deals with horizontal information and which ones deal with vertical information. However, there's an almost built-in mnemonic: look for the “o”.

Sine is the vertical length of the triangle. Tangent deals with coordinates when scaled up to the vertical tangent line. Secant deals with scaling factors up to the vertical tangent.

On the other hand, cosine is the horizontal length of the triangle. Cotangent deals with coordinates when scaled up to the horizontal tangent line. Cosecant deals with scaling factors up to the horizontal tangent.

Do you see what I mean by “looking for the o”? The words horizontal, cosine, cotangent, and cosecant all have an o in them, so they all go together.

Similarly, none of the words vertical, sine, tangent, and secant feature an o in them, so they all go together.

Looking for the letter o is an appropriate mnemonic for a circle, don't you think?

Another challenge is remembering the respective formulas. As mentioned before, SOHCAHTOA is the classic way to remember this, but that only gives 3 formulas.

Here's a lesser known yet more amusing mnemonic that gives all 6 formulas. Start by writing down the dividing lines, and writing “OOH AAH” above them:



“OOH AAH” is, no doubt, the sound you made upon first learning about unit circles. On the bottom, you're going to write “OOH AAH” again, but this time from right to left (as in “HAA HOO”):



From left to right, these are the formulas for the three vertical functions, sine (O/H), tangent (O/A), secant (H/A), followed by the three horizontal functions in the same order, cosine (A/H), cotangent (A/O), and cosecant (H/O).

You've also noticed that you can get some of these ratios simply by taking the inverse (dividing 1 by another number) of other factors. Tangent and cotangent are easy:



The ones beginning with t's are easy, so they can be thought of together. The ones featuring c's and s's are a little trickier:



When focusing on secant or cosecant, ignore the first s or c you see, and look for the second s or c. In the case of secant, you'd look at it as seCant. This C lets you know that it's the inverse of the function that begins with C - cosine!

With cosecant, you'd look at it as coSecant, and remember that this S it telling you that it's the inverse of the other S - sine!

Once you have that relationship down, here's a video that will take your knowledge of the trigonometric functions to the next level. It plays quickly, so you should pause it to read and understand everything it says:



Any further questions, class?